1.0 Abstract
There are many articles about CMAC Neural Network on the web, but none of them explain basic operation of CMAC clearly. The following writing introduces how CMAC works, examples of its implementation and coding CMAC in C++. It only requires basic mathematical knowledge to understand, but to learn very powerful technique for system control. Maybe open the door to future artificial intelligence research.
There are many articles about CMAC Neural Network on the web, but none of them explain basic operation of CMAC clearly. The following writing introduces how CMAC works, examples of its implementation and coding CMAC in C++. It only requires basic mathematical knowledge to understand, but to learn very powerful technique for system control. Maybe open the door to future artificial intelligence research.
CMAC stand for Cerebella Model
Articulation Controller
which is a
computational model to simulate biological cerebella and provides a
learning algorithm by updating weights of neurons base on the difference
between an output value and a desired output value in each training circle
(Hopefully not sounds too confusing).
Organization of CMAC
network;
the input space is quantized using a set of rectangular cells with finite
boundaries as shown above. The total collection of rectangular cells is divided
into C layers, referred as generalization parameter; Each layer is offset
relative to the others by the distance of Dj j, referred as quantization
interval; the width of individual rectangular cell is equal to C * Dj , known as input
generalization. Thus, CMAC network guarantees only number of C memory cells are
activated by one input.
In
the example of Figure 1, the CMAC network has 3 layers, so the generalization parameter C
is equal to 3; quantization
interval Dj is 1; Width of each rectangular cell known as
input generalization C *Dj is equal to 3.
Input space from 0 to 23.
Regulations of
CMAC arrangement:
CMAC network can be arranged with different number of layers; width of
rectangular cell and quantization interval, and can has several input spaces
for multi-input operation. On the condition that C parallel layers are offset
to each other with distance of Dj , the width of each rectangular cell is
equal to C * Dj , the input space
is large enough to cover all input values of specific application.
In CMAC operations, each memory cell can be
assumed as an on-off type of entity, which is initially empty and all the memory cells have a zero value. If
a memory cell is activated, its value is then equal to the value of adjustable
weight produced by previous training cycle add on current stored value.
Any input value falls within the range
of some adjacent cells are activated, and these excited
cells contain stored values. The sum of these values
produces an overall output of CMAC network.
During CMAC training, the difference between
CMAC output and desired output is divided by number of activated
cells, this value also known as adjustable weight which is added on
each of the activated cells, leave the other memory cells unchanged. After number
of learning cycles with different tanning data pairs such as input
and desired output, the value of each individual cell is adjusted in order to
reduce output error, so CMAC can produce an output ever close to desired
output.
The
Cerebellar Model Articulation Controller (CMAC) neural network is capable of
learning nonlinear functions extremely quickly due to the local nature of its
weight updating. The rectangular shape of CMAC receptive field functions,
however, produces discontinuous (staircase) function approximations without
inherent analytical derivatives. The ability to learn both functions and their derivatives
is important for the development of many on-line adaptive filter, estimation,
and control algorithms.
In follow demonstration, the
CMAC is trained to solve
nonlinear equation: y = x2,
where X is the input of CMAC and Y is the output of CMAC. With 3 pairs of training data input x = 10,
11, 12 and Output y = 100, 121, 144, CMAC adjusts value of excited cells to
reduce output error at each training cycle.
The output produced by CMAC network is given by:
y
is output produced by CMAC.
Wi
is current weight value stored in each activated memory cell.
C is total number of activated cells by the input.
The adjustable weight value for activated cells at each
training cycle is given by
C is total number of activated cells by the input.
C is total number of activated cells by the input.
DW
is adjustable weight value for activated cells.
y
is output produced by CMAC.
The
weight values of the activated cells are updated at each training cycle by
following equation:
Wj+1
is updated weight value of the activated cell after the training cycle.
Wj
is current weight value stored in each activated memory cell.
DWj is adjustable
weight value for activated cells.
Training cycle 1:
Input x = 12, desired output yd = 122 =
144; C = 3 activated cells V, M, E as shown in figure above. Since it is
non-training CMAC network, we mark the activated cells as
V0, M0, E0 = 0, 0, 0
respectively. The subscript indicates how many times the
activated cells have been trained.
CMAC output: = ( V0 +M0 + E0 ) = ( 0 + 0 + 0) = 0
= ( V0 +M0 + E0 ) = ( 0 + 0 + 0) = 0
Training cycle 3:
Figure 8 shows the feed-forward path of the Feedback error control scheme. If the CMAC controller is a perfect inverse model of the dynamic system, it can maintain y(t) = yd (t) indefinitely for t > 0. In other words, it can control the system perfectly by itself.
CMAC output:
 = ( V0 +M0 + E0 ) = ( 0 + 0 + 0) = 0
= ( V0 +M0 + E0 ) = ( 0 + 0 + 0) = 0
Adjustable weight value for activated
cells: DW = 1/C ( yd – y ) =
1/3 (144 - 0) = 48
Updated weight value of the activated
cell after the training cycle
Wj+1
= Wj + DWj
for updated cells V1 = 0+48 = 48, M1 = 0+48 = 48, E1
= 0+48 = 48
For the non-training CMCA network, Output
error = yd – y = 144 -0 = 144.
Training cycle 2:
Adjustable
weight value for activated cells: DW = 1/C ( yd – y ) = 1/3 (121
- 96) = 8.3
Updated
weight value of the activated cell after the training cycle
Wj+1
= Wj + DWj
for updated cells
U1
= 0+8.3 = 8.3, M2 = 48+8.3 = 56.3, E2 = 48+8.3 = 56.3
Output error = yd –
y = 121 – 96 = 25.
Training cycle 3:
As Figure 3 shows, input x = 10, desired output yd =
102 = 100; C = 3 activated cells U, M, D as shown in figure above.
We mark the activated cells as U1, M2, D0 =
8.3, 56.3, 0 respectively.
Adjustable
weight value for activated cells: DW = 1/C ( yd – y ) = 1/3 (100 –
64.6) = 11.8
Updated
weight value of the activated cell after the training cycle
Wj+1
= Wj + DWj
for updated cells
U2
= 8.3 +11.8 = 20.1, M3 = 56.3+11.8 = 68.1, D1 = 0+11.8 = 11.8
Output
error = yd – y = 100 – 64.6= 35.4
Repeat training data input x = 10, 11, 12 and
Output y = 100, 121, 144 again
Input x = 12, yd = 144;
activated cells V, M, E, marked as V1, M3, E2
= 48, 68.1, 56.3
Wj+1
= Wj + DWj
for updated cells
V2
=
48 + (-9.47) = 38.53, M4 = 68.1 + (-9.47) = 58.63, E3
= 56.3 + (-9.47) =
46.83
Output
error = |yd – y| = |144 – 172.4|
=
28.4
Training cycle 5:
Input x = 11, yd = 121; activated cells U, M, E,
marked as U2, M4, E3 = 20.1, 58.63, 46.83
Wj+1
= Wj + DWj
for updated cells
U3 = 20.1 + (-1.52) = 18.58, M5 = 58.63
+ (-1.52) = 57.11, E4 = 46.83 + (-1.52) = 45.31
Output
error = |yd – y| = |121 – 125.56| = 4.56
Training cycle 6:
Input x = 10, yd = 100; activated cells U, M, D,
marked as U3, M5, D1 = 18.58, 57.11,
11.8
Wj+1
= Wj + DWj
for updated cells
U4 = 18.58 + 4.17 = 22.75, M6 = 57.11
+ 4.17 = 61.28, D2 = 11.8 + 4.17 = 15.97
Output
error = yd – y = 100 - 87.49 = 12.51
Testing and Training cycle 7:
Repeat training data input x = 10, 11, 12 and Output y =
100, 121, 144 again
Input x = 12, yd = 144; activated cells V, M, E,
marked as V2, M6, E4 = 38.53, 61.28, 45.31
DW
= 1/C ( yd – y ) = 1/3 (144 - 145.12) = -0.37
Wj+1
= Wj + DWj
for updated cells
V3 = 38.53 + (-0.37) = 38.16, M7 = 54.46
+ (-0.37) = 54.09, E5 = 45.31 + (-0.37) = 44.94
Output
error = |yd – y| = |144 - 145.12|= 1.12
Testing and Training cycle 8:
Input x = 11, yd = 121; activated cells U, M, E,
marked as U4, M7, E5 = 22.75, 54.09, 44.94
CMAC output: = ( U4,+ M7 + E5 ) = (22.75 + 54.09 +44.94) = 121.78
= ( U4,+ M7 + E5 ) = (22.75 + 54.09 +44.94) = 121.78
CMAC output:
 = ( U4,+ M7 + E5 ) = (22.75 + 54.09 +44.94) = 121.78
= ( U4,+ M7 + E5 ) = (22.75 + 54.09 +44.94) = 121.78
DW
= 1/C ( yd – y ) = 1/3 (121 - 121.78) = -0.26
Wj+1
= Wj + DWj
for updated cells
U5 = 22.75 + (-0.26) = 22.49, M8 = 54.09
+ (-0.26) = 53.83, E6 = 44.94 + (-0.37) = 44.57
Output
error = |yd – y| = |121 - 121.78| = 0.78
Testing and Training cycle 9:
Input x = 10, yd = 100; activated cells U, M, D,
marked as U5, M8, D2 = 22.49, 53.83, 15.97
CMAC output: = ( U5,+ M8 + D2 ) = (22.49 + 53.83 +15.97) = 92.29
= ( U5,+ M8 + D2 ) = (22.49 + 53.83 +15.97) = 92.29
CMAC output:
 = ( U5,+ M8 + D2 ) = (22.49 + 53.83 +15.97) = 92.29
= ( U5,+ M8 + D2 ) = (22.49 + 53.83 +15.97) = 92.29
DW
= 1/C ( yd – y ) = 1/3 (100 - 92.29) = 2.57
Wj+1
= Wj + DWj
for updated cells
U6 = 22.49 + (2.57) = 25.06, M9 = 53.83 + (2.57) = 56.4, D3 = 15.97+ (2.57) = 18.54
Output
error = yd – y = 100 - 92.29 = 7.71
Result Analysis
After 9 training cycle, the
CMAC network reduces output error significantly, the
network produces an accurate approximation to the
equation of y =x2. For training data pair input x = 12 and output y
=144, 100% error rate between CMAC output and real output at training cycle 1.
However, the error rate reduce to (1.12/144) % = 0.7% at training cycle 7.
To test CMAC with an input query x = 12, what
is the output y = x2, the CMAC response is 145.12, input x = 11, the CMAC respose is 121.78, input x =10
the CMAC response is 92.29. The reason for significant amonut of error with
query input 10 is the CMAC hasn’t been fully trained, there are still large
portion of memory cells haven’t been updated.
A fully trained CMAC network is capable of reducing error rate to less
than 1% for majority of input queries within the range of its input space.
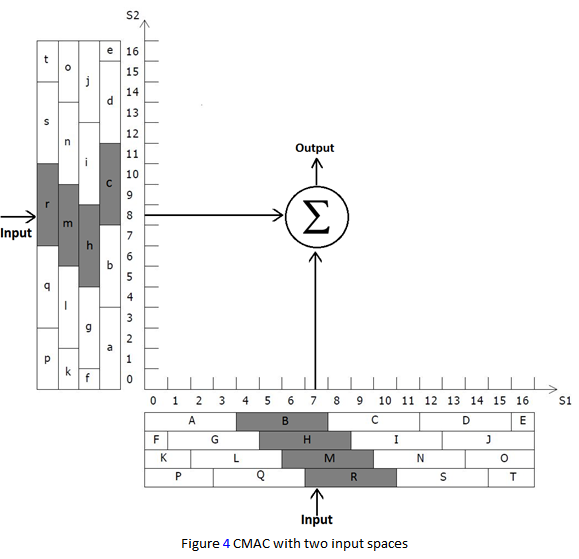
2.2 CMAC with Multi-input Spaces
CMAC network can has several input spaces for
multiple inputs operation. The following CMAC network has two input spaces: S1
from 0 to 16, S2 from 0 to 16. Each input space is arranged with 4 layers,
quantization interval Dj is 1;
Width of each rectangular cell known as input generalization C * Dj, is equal to 4.
CMAC for Multi-input Operation
The CMAC process multiple inputs function
is in similar fashion as single input operation. For example, train the above
CMAC network to approximate equation y = x2 +z2, which
has two input parameters X and Z.
Propose training data pair of input state (7, 8) and output 113;
activated memory cells are B, H, M, R and c, h, m, r.
Note: For
multi-input state, the total activated cells are equal to total number of layers
in all input spaces.
Training cycle 1:
The CMAC output would be sum of weight value in all 8
excited cells. CMAC output:
y = (B0 + H0 + M0
+R0 + c0 +h0 + m0 + r0)
= (0+0+0+0+0+0+0+0) =0
The adjustable weight value is the difference the difference between
CMAC output and desired output divided by number 8 of activated
cells:
DW
= 1/8(0-113) =14.125
Updated
weight value of 8 activated cell after this training cycle
Wj+1
= Wj + DWj B1 = 14.125, H1
= 14.125, M1
= 14.125, R0
= 14.125, c1
=14.125,
h1 = 14.125, m1 =14.125, r1 = 14.125.
The rest of training procedure is similar to above. After
number of training sessions with different training data pairs, the CMAC
network converge on the function y = x2 +z2 with excellent
accuracy.
DW = 1/ C (yd - y) b
b is a constant training gain also refer to learning rate to prevent over shoot. If b is 1.0, the weights are adjusted to force the network output y to be exactly equal to the training target yd. If b is 0.5, the network output is adjusted to fall halfway between the old output value and the training target. If b is 0.0, the weights are not changed. For simplify the demonstration of CMAC operation, the Training gain was not introduce during previous CMAC calculation.
2.3 Training gain
DW = 1/ C (yd - y) b
b is a constant training gain also refer to learning rate to prevent over shoot. If b is 1.0, the weights are adjusted to force the network output y to be exactly equal to the training target yd. If b is 0.5, the network output is adjusted to fall halfway between the old output value and the training target. If b is 0.0, the weights are not changed. For simplify the demonstration of CMAC operation, the Training gain was not introduce during previous CMAC calculation.
3.0 CMAC for System Pattern Mapping:
From pervious CMAC computation, CMAC is excellent technique to
approximate structure of unknown system. For instance, the governing equation
for unknown system is
With different input and output data pairs, the CMAC network can be
trained to converge on the function, thus to represent the unknown system.
3.1 CMAC learn the inverse model of unknown
system
In a standard control scheme in Figure 6, the controller needs to be the
perfect inverse model of the system to maintain y(t) = yd(t), so the
system is under control.
Generally, it is hard to determine the function of unknown
system. Even if the function is known exactly, computing an inverse can be
difficult. CMAC network can be trained to
approximate unknown system. Thus, train CMAC neural network to approximate
inverse model of unknown system is effective approach of designing system
controller.
3.2 CMAC Feedback Error Controller:
As Figure 7 shows, the CMAC
neural network is implemented with Feedback error control scheme, which was
originally proposed by Kawato. The CMAC feedback error scheme has two main
components, the feed-forward path through CMAC network and the feedback path
through PID controller (proportional plus derivative).
In general the System is
mostly concerned with non-linear dynamic system such as multivariate robotic
manipulator or temperature control system. X(t) is the control
signal and y(t) is the output of the System, yd(t) is the desired value of y(t), supplied by some
external agent. The purpose of the controller is to maintain y(t)
follows yd(t), so the System
is being controlled.
In the beginning of
control process, the non-trained CMAC network of feed-forward path contains empty
memory cells, so it has no knowledge about the system. With a desired reference
value as the input query, the CMAC controller output control signal xc(t) = 0 to drive the System. Thus, the CMAC
controller has no control on the System at this
moment.
Simultaneously, the PID controller of feedback
path generates the control signal xp(t) ≠ 0 to drive the System, based on the difference
between desired reference value yd(t) and current system output y(t). The xp(t) is also the training signal error e given
to CMAC for updating its weight values, so the CMAC could produce better
signal xc(t) in
next control iteration.
As the control process running, the System
output y(t) is driven toward desired output yd (t).
Equally xp(t) is
getting smaller, PID
controller will have less to do. Once the y(t) = yd(t), then
IPD output xp(t)
= 0. In
this case the system is perfectly controlled by CMCA controller, so no
adjustment to CMAC is
necessary. Hence, CMAC
has been trained to become the inverse model of the System. During control process, there
is a transfer of control influence from the feedback PID controller loop xp(t) to the feed-forward
CMAC controller xc(t).
When CMAC has fully control on the system, it can response
to number of different desired set-point yd(t) as input query, provides instant control signals xc(t) to drive y(t)
along a desired trajectory yd (t). The PID controller of feedback
path stabilizes the system by compensating for any imperfections in CMAC controller or any disturbances from
the System. Thus, the PID controller supervise
CMAC learning by providing correction control signals xp(t) to the System, when y(t) and
yd(t) diverge.
To further understand advantages of CMAC Feedback Error
Controller in Figure 7, the feed-forward and
feedback paths are examined separately.
The Feed-forward Path:
Figure 8 shows the feed-forward path of the Feedback error control scheme. If the CMAC controller is a perfect inverse model of the dynamic system, it can maintain y(t) = yd (t) indefinitely for t > 0. In other words, it can control the system perfectly by itself.
However, the CMAC controller is only an approximation to the
inverse model of the system, so it can never be made perfect. In addition, any
noise or disturbance in the system will cause y(t) and yd (t) to diverge. Thus, a
pure feed-forward controller is not practical. It’s necessary to have feedback
path stabilizes the system by compensating for any
imperfections in CMAC
or any disturbances.
The Feedback Path:
Figure 9 shows the feedback path
of the controller, which is constructed with a PID controller.
Generally, if the PID
controller parameters (the gains of the proportional, integral and derivative
terms)
are chosen well enough, stable control can be achieved.
The problem faced with PID controller is that they are
linear and in particular symmetric.
When PID controllers used alone with non-linear dynamic
system (such as robotic manipulator or temperature control system), can give
poor performance. For instance, excessive gain of PID
controller cause instability such that system output overshoot, oscillates around
the desired reference value and increases settling time. While reduce gain to prevent overshoot cause
decrease performance, have significant lag in responding to large disturbances.
Therefore, the most significant improvement is to incorporate feed-forward CMAC
with knowledge about the system, and using the PID only to control error.
In addition, the linear PID controller can
only be chosen for one optimal operating point of yd(t). While the fully trained CMAC
controller is capable to handle different desired set-points yd(t). Since the CMAC has the main
control influence on the system and the PID is only used for minor adjustment,
the control system is unlikely to oscillate, thus improving the system response
and stability.
Feed-forward and feedback together
The
control system performance can be improved by combining the feedback path with feed-forward path. The
feed-forward path often provides the major portion of the controller output x(t). The PID controller is primarily response to whatever
difference or error remains between the desired reference value yd (t) and the System output value y(t).
The innovation of feedback-error control is that the
training signal error e given
to CMAC is just the feedback
signal xp(t) generated by
PID controller. CMAC
controller could learn to produce better control signal xc(t) along with the PID output to improve the
overall system performance.
CMAC neural network is the modern approach of building adaptive control
system, which has the abilities to learn through training examples and
accomplish pattern mapping for unknown system. Thus, CMAC facilitates the
process of control system design compared with the conventional approach
of finding the governing equation of unknown system.
CMAC has been successfully implemented in a number
of applications, including robot arm control, induction Motor Driver and learning nonlinear thruster
dynamics to control an underwater robotic vehicle.
4.1 Robot Arm Learn Playing
a Toy Yo-Yo
In the following project, the CMAC Feedback Error Controller
has been implemented into a robotic system, so the robot arm can
learn to control oscillatory motion of a yoyo at desired level.
In the experiment, option 2 is the alternative
design configuration to simplify the control algorithm for moving the robot arm
and facilitates software implementation, so the project could primary focus on
robotic arm learning strategies.
When yo-yo is bouncing up and down, the
kinetic energy is converted to potential and vice versa. It dissipates the
energy at the bottom impact and due to the friction between the string and the
yo-yo. To obtain oscillatory motion it is necessary to supply energy to the
system. As the robot arm goes up, energy is transfer to yoyo motion. Without
external energy, the yoyo oscillation will eventually goes off.
Note: The other robotic yoyo
control strategies are not mentioned in this article. Complete details about
this project on article “Robot Arm Learns Playing a Toy Yoyo” and Project video
link:
http://skyocean117.blogspot.co.nz/2013/12/robot-arm-learns-playing-toy-yoyo.html
http://skyocean117.blogspot.co.nz/2013/12/robot-arm-learns-playing-toy-yoyo.html
4.2 CMAC Feedback
Error Controller for yoyo control
When yo-yo is bouncing up and down, the kinetic energy is
converted to potential and vice versa. It dissipates the energy at the bottom
impact and due to the friction between the string and the yo-yo. To obtain
oscillatory motion it is necessary to supply energy to the system. As the robot
arm goes up, energy is transfer to yoyo motion. The fast robot arm moves the
higher yoyo reaches.
In Figure 11, the controller has been implemented into robot
arm and yoyo is the system being controlled. The purpose of this control
process is that the robot arm make upward motion at speed of xp(t)
to maintain top height of yoyo y(t) at desired level yd(t).
x(t) indicates top speed m/s during the upward motion of tip
of robot arm where yoyo’s string is attached, With a pre-defined moving pattern,
the tip of robot arm move up by 11.7cm, and has initial 20% of the distance for
constant acceleration to top speed of x(t) m/s, then the last 20% distance to
decelerate to stop, and then move back to default position before next yoyo
cycle. The robot arm with fix movement will supply same amount energy to the
yoyo, which cannot response to the disturbance of yoyo motion; so cannot
control the amplitude of yoyo, an adaptive controller is needed.
The complete mathematical model of a yo-yo is very complicated;
there are many difficulties to computing an inverse model of yoyo motion. In
addition, the presence of undesired yoyo motion such as swinging, yawing and
pitching create large disturbance which dissipate extra energy during yoyo
oscillation, thus an adaptive CMAC Feedback Error Controller is implemented
as following diagram.
Figure 12 shows the CMAC Feedback Error Controller has been
implemented into the robotic arm system. The robotic system can learn to produce
accurate speed xc(t) of upward motion to maintain y(t) = yd(t).
The Feedback Error control scheme applies to both continuous-time system and
discrete-time systems. The (t) represents the number of oscillatory cycle of
yoyo, but not time interval. The Ultrasonic Sensor measures the top height of
yoyo in each cycle.
In the beginning of control process, the non-trained CMAC
network contains empty memory cells, so it has no knowledge about the yoyo
system. It receives an input query that the selected top height of yoyo up-down
motion at yd(t) (82 cm is the highest position that yoyo can reach before
hit top constraint ), the CMAC controller output speed xc(t)=0 m/s,
which suggest the upward motion of robot arm is 0 m/s. Thus, no energy is transfer to the yoyo.
Simultaneously, the Ultrasonic Sensor measured the highest
point y(t) that the yoyo has reached during last oscillatory cycle. The PID
controller generates the speed command such as xp(t) = 1.1m/s based on the difference
between yd(t) and y(t). The sum of xc(t)
and xp(t) is the upward
motion speed x(t) of robot arm. Hence, robot arm move up at top seed 1.1 m/s
during upward motion, and this upward motion supply energy to the yoyo.
The xp(t)
produce by PID controller is
also the training signal error e given to CMAC for updating its weight
values, so the CMAC could learn
to produce correct speed command xc(t) in next oscillatory cycle.
After number of oscillatory
cycles, the System output y(t) is driven toward desired output yd (t).
Equally xp(t) is
getting smaller, PID controller will
have less to do. Once the y(t) = yd(t), then IPD output xp(t) = 0. In this case, the fully trained
CMAC controller provide the major portion of the speed output x(t), its memory
cells contain knowledge about the yoyo system, and using the PID controller to
stabilize the by compensating for any disturbances from yoyo’s undesired motion.
The other advantage of implementing CMAC Feedback Error
Controller for yoyo control is that the CMAC neutral network can provide
optimal control for several different input queries. E.g. the desired top
height of yoyo can be maintained at different level such as 60cm, 65, 70cm or
75cm above bottom position. The fully trained CMAC can provide instant output
based on which desired yoyo top height is selected. While use the PID
controller alone on Feedback path, it can only handle for one desired yoyo top
height.
Video about CMAC feedback error controller for yoyo control is on following web link, time from 0:00 to 3:20: http://www.youtube.com/watch?v=yJMeYc_eHtI
4.3 Experiment Setup
The experiment
devices induce: a plastic yoyo, a load cell measure tension force on the
string, ultrasonic Sensor to measure the position of yo-yo in real time, so
the robot arm can make upward motion at right moment.
Stepper motor drive one joint the robot arm, yoyo’s string
go through a rectangle wooden structure, so yoyo can move directly up and down
and stay in the sensing area of ultrasonic sensor.
The
purpose of this project is to develop algorithms
and strategies for the robot arm to learn playing different yo-yos. After studied the way humans operate a yoyo, two main control
strategies for playing yo-yo successfully.
- The upward
motion of robot arm should start just before the yo-yo reaches its bottom
position. In this way, the yo-yo
gain maximum energy for up-down motion.
- By changing the top speed of robot arm
during upward motion, the amplitude of yo-yo motion can be maintained at
desired level.
Since yoyos are made of different materials, has different speed of
their spin, the string length and undesired motion such as swinging, yawing and pitching, it requires
adaptive control strategy. Human operator can adjust quickly to play different
yo-yo successfully, but the robot arm with fixed movement cannot operate
different yo-yos with different string length. Thus, an adaptive
controller with the knowledge about robotic yoyo system is needed.
The following tasks have been achieved in this project:
- Implement CMAC feedback error controller to provide accurate speed for upward motion to maintain the top height of yo-yo at desired level.
- The robot arm can learn playing different yo-yo with self-turning process to find out when is best moment for upward motion.
- The robot arm also can learn playing different yoyo from human demonstration.
6.0 Reference
Video about robot arm learns playing a yoyo on following link:
Complete details about this project on
article “Robot Arm Learns Playing a Toy YoYo”
Complete details about how to program CMAC in C++, can view
article: “UNH_CMAC Version 2.1”
5.0 Coding CMAC in C++
The two following code files contain source code of CMAC. unh_cmac.h contains CMAC functions, cmacdemo.c is calling these functions to train CMAC to learn a nonlinear function
z = sin(x + y).
z = sin(x + y).
More details about how to program CMAC in C++, can view article: “UNH_CMAC Version 2.1”
The University of New Hampshire Implementation of the Cerebellar Model Arithmetic Computer – CMAC
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
/* cmacdemo.c */
/*
This
test program exercises some of the CMAC calls
It
trains in a simple nonlinear function:
The
program sits in a loop, testing at 100 random points
and
training at 100 random points, until any key is hit.
After each testing cycle (100 random points) the
approximation error and memory usage is
displayed.
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <fcntl.h>
/* Commented out by Patrick van der Smagt
20/08/96 PvdS */
/*#include <io.h>*/
/* Commented out by Patrick van der Smagt
20/08/96 PvdS */
/*#include <conio.h>*/
#include <sys/types.h>
#include <sys/stat.h>
#include "unh_cmac.h"
static int state[2], quant[2] = {10,10},
response[2];
static int cmac_id;
static int num_state = 2, num_resp = 1,
num_cell = 16;
static int mem_size;
static int beta = 2;
void test(void);
void train(void);
main()
{
static
int i,j,k;
static
int index;
static
float x,y,z;
static
float pi = 3.14159;
static
float error_r, mag;
/*
allocate the CMAC
*/
/*
2 inputs, 1 output, generalization = 16 */
cmac_id
= 0;
while(!cmac_id)
{
printf("\nInput
CMAC memory size (e.g. 3000): ");
scanf("%d",&mem_size);
cmac_id
= allocate_cmac(num_state, quant, num_resp, num_cell,
mem_size,
LINEAR, 0);
if
(!cmac_id) {
printf("CMAC allocation
failure!\n");
}
}
clear_cmac_weights(cmac_id);
test(); /* test
CMAC */
i=0;
while(++i
< 200) {
train(); /*
train CMAC */
test(); /*
test CMAC */
}
/*
save CMAC weights in file */
printf("\nSaving
CMAC weights in file\n");
save_cmac(cmac_id,
"weights.dat");
/*
now clear the weights and retest (showing forget) */
printf("\nClear
CMAC weights and test\n");
clear_cmac_weights(cmac_id);
test();
/*
unsave CMAC weights from file and test again */
printf("\nRestore
CMAC weights and test\n");
deallocate_cmac(cmac_id);
cmac_id
= restore_cmac("weights.dat");
test();
/*
de-allocate the CMAC and exit */
deallocate_cmac(cmac_id);
remove("weights.dat");
}
void test(void)
{
static
int i,j,k;
static
float x,y,z;
static
float pi = 3.14159;
static
float error_r, mag;
/* test at 100 random x,y points */
error_r = 0.0;
mag = 0.0;
for (k=0; k<100; ++k) {
x
= pi * (float)rand() / 32768.;
y
= pi * (float)rand() / 16384.;
z
= 1000.0 * sin(x + y);
state[0]
= (int)(200.0 * x);
state[1]
= (int)(200.0 * y);
cmac_response(cmac_id,
state, response);
error_r
+= fabs( z - (float)response[0] );
mag
+= fabs( z );
}
printf("Percent Error = %5.1f,",
(100.0 * error_r/mag));
printf(" Memory Used = %6d\n",
cmac_memory_usage(cmac_id));
}
void train(void)
{
static
int i,j,k;
static
float x,y,z;
static
float pi = 3.14159;
/* train at 100 random x,y points */
for (k=0; k<100; ++k) {
x
= pi * (float)rand() / 32768.;
y
= pi * (float)rand() / 16384.;
z
= 1000.0 * sin(x + y);
state[0]
= (int)(200.0 * x);
state[1]
= (int)(200.0 * y);
response[0]
= (int)z;
train_cmac(cmac_id,
state, response, beta, 40);
}
}
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
/* *************************************** */
/*
unh_cmac.h - CMAC function prototypes
*/
/* *************************************** */
/* Define some commonly used CMAC receptive
fields geometries */
#define ALBUS (int)'A'
#define RECTANGULAR (int)'R'
#define LINEAR (int)'L'
#define SPLINE (int)'S'
#define CUSTOM (int)'C'
/*
---------------------------------------------------------------------------*/
int allocate_cmac(int num_state,int
*qnt_state,
int num_resp, int num_cell,
int memory, int rfield_shape, int
collision_flag);
/*
Returns:
CMAC ID upon success (1-7), 0 upon failure
DESCRIPTION:
This procedure allocates a CMAC with the
parameters defined as follows:
num_state dimension of the
input state vector
qnt_state[] quantization
vector
num_resp dimension of the
output response vector
num_cell generalization
parameter
memory number of vectors in the CMAC
memory
rfield_shape one of the above
defined constants for RF functions
collision_flag TRUE if
collisions OK, FALSE for no collisions
The quantization vector is a scalling vector
with the same dimension as
the input state vector. Essentially, in interpretating the state
vector the
CMAC routines first divide each component of
it with the corresponding
component of the quantization vector.
The procedure returns a number, referred to
as the CMAC ID, used in later
calls to identify which CMAC is being
accessed. An ID of 0 indicates that
either the memory allocation failed, or the
maximum number of simultaneous
CMACs, set by cmac_init, has been exceeded.
---------------------------------------------------------------------------*/
int train_cmac(int cmac_id, int *state, int
*respns, int beta1, int beta2);
/*
Returns:
1 if success, 0 upon failure
DESCRIPTION:
This procedure trains the CMAC memory, where:
cmac_id identifies the cmac, (the
number returned by alloc_cmac()).
state points to the training
input state vector.
respns points to the training
output response vector.
beta1 is the response error
training gain expressed as a right shift
factor (i.e. 0 = 1.0, 1 = 0.5, 2 = 0.25, ...).
beta2 is the weight
normalization training gain expressed as a right
shift factor (i.e. 0 = 1.0, 1 = 0.5, 2 = 0.25, ...).
The procedure returns TRUE (1) if completed
successfully, FALSE (0) if the
cmac_id is incorrect.
---------------------------------------------------------------------------*/
int cmac_response(int cmac_id, int *state,
int *respns);
/*
Returns:
1 if success, 0 upon failure
DESCRIPTION:
This procedure returns the CMAC response,
where:
cmac_id identifies the cmac, (the
number returned by alloc_cmac()).
state points to the training
input state vector.
respns points to the training
output response vector.
The procedure returns TRUE (1) if completed
successfully, FALSE (0) if the
cmac_id is incorrect.
---------------------------------------------------------------------------*/
int clear_cmac_weights(int cmac_id);
/*
Returns:
1 if success, 0 upon failure
DESCRIPTION:
This procedure clears the CMAC memory to all
0 values (forgets past training)
where cmac_id is the identification number
returned by alloc_cmac().
The procedure returns TRUE (1) if completed
successfully, FALSE (0) if the
cmac_id is incorrect.
---------------------------------------------------------------------------*/
int deallocate_cmac(int cmac_id);
/*
Returns:
1 if success, 0 upon failure
DESCRIPTION:
This procedure de-allocates the CMAC memory,
where cmac_id is the
identification number returned by
alloc_cmac().
The procedure returns TRUE (1) if completed
successfully, FALSE
(0) if the cmac_id is invalid.
---------------------------------------------------------------------------*/
int cmac_memory_usage(int cmac_id);
/*
Returns:
number of non-zero weight vectors in a CMAC memory
DESCRIPTION:
This procedure returns the number of CMAC
memory vectors that
have been used in training since the last
call to forget, where cmac_id is
the identification number returned by
alloc_cmac().
The procedure returns FALSE (0) if the
identification is incorrect OR if the
memory is all 0's.
---------------------------------------------------------------------------*/
int get_cmac(int cmac_id, int index, int
*buffer, int count);
/*
Returns:
number of weight vectors transferred
DESCRIPTION:
This procedure transfers vector values
directly from the CMAC memory to
the buffer specified, where:
cmac_id is the CMAC
identification number.
index is a legal index into the
CMAC memory (in vector offset
units, 0 = first vector, 1 = second vector, etc.).
buffer is a pointer to a buffer
to which the CMAC memory is to
be transfered.
count is the number of
sequential vectors to be transfered to
the buffer.
---------------------------------------------------------------------------*/
int put_cmac(int cmac_id, int index, int
*buffer, int count);
/*
Returns:
number of weight vectors transferred
DESCRIPTION:
This procedure transfers vector values directly
to the CMAC memory from the
buffer specified, where:
cmac_id is the CMAC
identification number.
index is a legal index into the
CMAC memory (in vector offset
units, 0 = first vector, 1 = second vector, etc.).
buffer is a pointer to a buffer
from which the CMAC memory is to be
transfered.
count is the number of
sequential vectors to be transfered from
the buffer.
---------------------------------------------------------------------------*/
int adjust_cmac(int cmac_id,int *state,int
*drespns,int beta1);
/***************************************************************************
* adjust()
*
* *
* Input: cmac_id, state[], drespns[],
beta *
* Output: ap[]
*
*
*
* Purpose: Train ap[] cells based on latest
experience *
* state[] is mapped to
indexes[] by stoap() *
*
*
***************************************************************************
---------------------------------------------------------------------------*/
int map_cmac_input(int cmac_id,int *state,int
*weights[], int *rfmags);
/***************************************************************************
* map_cmac_input()
*
*
*
* Input: cmac_id, state[] *
* Output: *weights[], rfmags[] *
*
*
* Purpose: returns pointers to the weight vectors
mapped *
* by
the input vector state[], and the associated
*
* receptive
field magnitudes
*
*
*
***************************************************************************
---------------------------------------------------------------------------*/
int set_cmac_rf_displacement(int cmac_id,int
*buffer);
/***************************************************************************
* set_displacement()
*
*
*
* Input: cmac_id, displacement vector *
* Output: none *
*
*
* Purpose: writes displacement vector to CMAC
storage *
*
*
***************************************************************************
---------------------------------------------------------------------------*/
int set_cmac_rf_magnitude(int cmac_id,int
*buffer);
/***************************************************************************
* set_rf_table()
*
*
*
* Input: cmac_id, RF function table *
* Output: none *
*
*
* Purpose: writes RF magnitude table to CMAC
storage *
*
*
***************************************************************************
---------------------------------------------------------------------------*/
int save_cmac(int cmac_id,char *filename);
/***************************************************************************
* save_cmac()
*
*
*
* Input: cmac_id, file name *
* Output: none *
*
*
* Purpose: writes all of CMAC storage to a
file *
* *
***************************************************************************
---------------------------------------------------------------------------*/
int restore_cmac(char *filename);
/***************************************************************************
* restore_cmac()
*
*
*
* Input: file name *
* Output: cmac_id, or FALSE (0) on failure *
*
*
* Purpose: restores all of CMAC storage from a
file *
*
*
***************************************************************************
---------------------------------------------------------------------------*/
















Wow ! You have a blog too ! Impressive. This is a pretty long article and lot of C++ code as well :).
ReplyDelete